By default, Full is selected in the Analysis Option drop-down list, and if you do not change this option, a full dynamic random sea analysis is performed as a precursor to the fatigue analysis. This analysis corresponds to the dynamic analysis you have defined on the Installation Stage tab.
The maximum duration of this dynamic analysis is equal to the duration that you specify on the Installation Stage tab via the Start Time and End Time parameters. However, you have the option of terminating the analysis before this time is reached if you are confident output statistics have reached ‘steady state’ and further simulation is unnecessary; this option is discussed in further detail later in the description of Plot of Maximum Variation in Restoring Force Statistics in the ‘Fatigue - Normal Lay - Outputs’ article.
While the dynamic analysis is in progress, timetrace output of axial force and y- and z-bending moment is automatically generated for each node in the pipeline section of interest. No database output is generated by default, to minimise disk space usage. However, the Generate Database Output drop-down list allows you to over-ride this if you want, in which case the normal dynamic analysis results are output for subsequent postprocessing.
If you want to use the results from a previously run analysis as a starting point for the fatigue computations, you can select Previous from the Analysis Option drop-down list. This allows you to skip the random sea dynamic analysis, and proceed directly to fatigue postprocessing using output stored from an analysis already run.
Once the dynamic simulation is complete, time histories of combined stress are generated for each of 8 points around the cross-section circumference at each node. Rainflow cycle counting is then used to transform each time history into a value of rate of fatigue damage. This process is carried out in 3 steps. Firstly, each time history is transformed into a list of stress ranges, in standard fashion. This stress range data is then output to a (binary) storage file, for possible use in a repeat fatigue analysis. At this stage the timetrace data file generated during the random sea analysis can optionally be deleted to save disk space. This option is facilitated by the Delete Stress History Timetraces drop-down list; the default is No, meaning the time histories are retained. Secondly, the stress range data is used to compute fatigue damage, taking into account the specified S-N Curve. Finally, fatigue damage values are divided by the total simulation length to give a rate of fatigue damage value for each of 8 points on the circumference at each node.
If you have set Generate Histogram Output to Yes, the stress range data is also sorted into the appropriate stress histogram bins. The bins are defined in the Histogram Bins dialog; please note that the lower bound of the first bin always has a zero value, so the entry in the first row of the Histogram Bins dialog defines the upper bound of the first bin. All entries following this define the upper bounds of the bin with the value in the previous row being used as the lower bound. If you choose to leave the Histogram Bins dialog empty a set of default bins is generated. Once the stress range data has been sorted into the defined stress bins, a nodal stress histogram data set is output to a CSV file. The CSV file name defaults to fatigue_hist.csv and contains the counted stress cycles for each bin at all 8 circumference points at every node.
If you want to use the stress range data from a previously run fatigue analysis, you can select Restart from the Analysis Option drop-down list. This allows you to skip the computations involved in generating time histories of combined stress for all the circumferential locations at each node, and also the transformation of these histories into stress ranges using Rainflow counting. In this way you can for example examine the effect of varying the S-N Curve. The Repeat fatigue analysis begins by reading the stress range file (presuming it exists, otherwise an error will be generated), and then proceeds to the calculation of fatigue damage rates and the rest of the fatigue calculations as before.
Using the weld locations on the vessel (specified via the Vessel Weld Locations button), and the computed fatigue damage rates, the governing weld on the vessel (that is, the weld with the largest damage rate) is identified. It should be noted that weld locations and nodes are not coincident in general, so identifying the critical fatigue damage rate typically involves cubic spline interpolation between nodal values. Subsequent weld locations are then identified in the catenary section, by incrementally adding the specified Pull Length to the location of the governing weld on the vessel.
Total fatigue damage occurring during installation is then calculated as follows. The number of fatigue calculation weld positions (comprising the governing weld position on the vessel and all subsequent locations in the catenary section), is counted to give the number of calculation steps required. For each weld location, the nearest node(s) are identified. Based on this, damage rates (around the circumference) are found for each weld location. The damage rates for each weld location are then multiplied by the specified Cycle Time, to give the fatigue damage occurring at each weld location for the duration between pulls. Looping over the number of calculation steps, the total fatigue damage occurring duration installation is obtained by summing the fatigue damage at each weld location.
If you have requested histogram outputs, a weld stress histogram is also accumulated for all 8 circumference points and from this a governing histogram is derived as well. This accumulation process is performed in a similar fashion to weld fatigue damage except nodal histograms are used in this instance rather than nodal damage rates. To elaborate, firstly the number of weld positions is calculated as per the previous paragraph. Then for each weld location, the nearest node(s) are identified. Based on this, the nodal stress histogram data is divided by the analysis duration in order to estimate bin variations over time, or ‘bin rates’ if you will. Using the ‘bin rates’ and suitable interpolation functions between the nodes, a profile of ‘bin rates’ along the pipeline is established for each bin at each of the circumference locations. Once the profile is defined, a weld stress histogram for all 8 circumferential points is calculated by multiplying the relevant ‘bin rates’ by the Cycle Time and adding up across each weld location; the governing weld stress histogram contains the maximum number of counted stress cycles for each bin across the 8 circumferential points.
Once the total fatigue damage is known, the duration that the suspended pipeline can be held stationary without exceeding the specified Allowable Fatigue Damage can be determined. The duration is calculated by subtracting the total calculated fatigue damage from the allowable fatigue damage. This difference is then divided by the maximum damage rate (that is, the highest damage rate from all weld locations), to give a maximum allowable standby time.
As a further output, the maximum fatigue damage rate for the touchdown point is estimated, by identifying a governing position in the touchdown region. Because the exact locations of welds in the touchdown region are unknown, all nodes within a Pull Length of the static touchdown point are considered. The maximum fatigue damage rate for the touchdown point is then assumed to be equal to that of the node with the highest fatigue damage rate in this region. An illustrative flowchart for the Normal Lay fatigue approach is provided in the figure below.
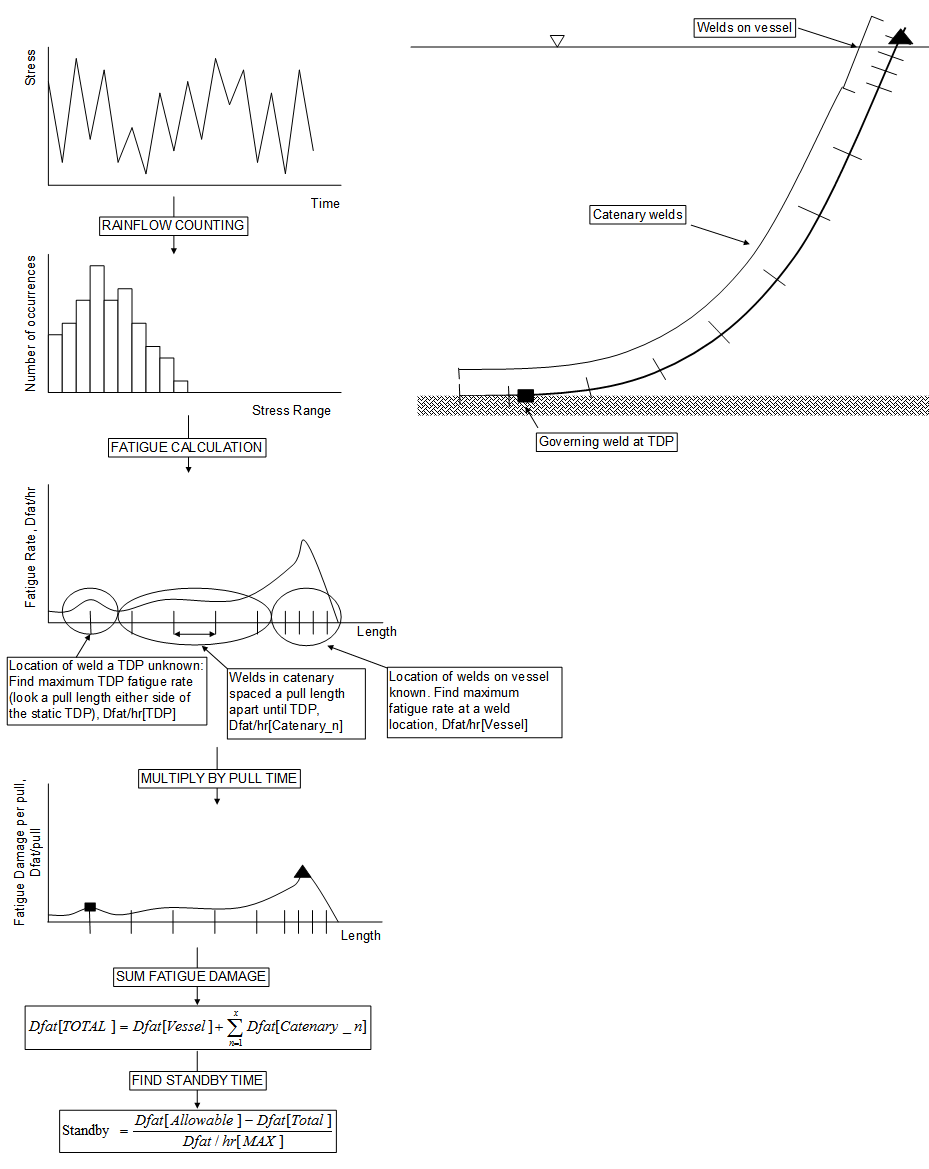
Flowchart for Normal-Lay Fatigue