The Material component is used to define the physical properties associated with a particular material.
It may be regarded as a basic building block for all models, and is typically referenced several times in a particular project by higher-level components. For example, a Material component might be created to model steel, and this could be used subsequently in the specification of Pipe Section and Cable components. Both linear and non-linear material specifications are available, with several format options provided for the latter case.
The Material theory can be found in this article while the following articles provide information on Material Data Inputs and Material Best Practice.
Linear materials are characterised by Young’s Modulus, Shear Modulus and Mass Density. You must input values for Young’s Modulus (E) and Mass Density (ρ) for all linear materials. PipeLay also requires a value for Shear Modulus (G), but this can be specified in one of the following ways:
•You directly input a value for Shear Modulus.
•You input a value for Poisson’s Ratio (ν) and PipeLay works out a value for G from E and ν using the standard relation.
There are a number of additional optional inputs. For example, you can input a Thermal Expansion Coefficient if you want to include temperature effects in your analysis. Specifying a value for Poisson’s Ratio includes Poisson’s ratio effects in your analysis. Other optional entries include Yield Strength, Allowable Stress and Allowable Strain values. These variables are only used in the generation of tabular output, as part of postprocessing, and have no effect on the finite element analysis.
There are three options available in PipeLay for defining non-linear material properties as follows:
▪Moment/Curvature relationship
The following points relate to all three specifications:
•Young’s Modulus (E) is a mandatory input in all cases. How this value is used depends on which of the three non-linear options is chosen.
•Shear Modulus (G) can be specified in the same way as for a linear material.
•A direct stress/strain curve can define both bending and axial response. E in this case is used only to define linear material properties for an initial static step, in which case it defines EI and EA for each pipe section on which the material is used. Where a user specified I value is supplied, the bending stiffness is defined as EIuser.
Otherwise, the user-specified stress/strain curve defines an N-δ (axial force-extension) curve and an M-κ(bending moment-curvature) curve for each pipe section. Note that the use of an N-δ curve can be controlled by a Nonlinear Axial Stiffness option, which if set to No results in a linear axial (EA) stiffness being used throughout rather than a curve. Where a user specified I value is supplied, the value is used to adjust the inner diameter to give an equivalent pipe section when calculating the M-κ(bending moment-curvature) curve. This diameter adjustment is for pipe stiffness only and result post-processing will be based on the actual pipe outer/inner diameters. With a stress/strain specification it is also possible to specify an Expected Tension value which is used to reduce the capacity of the M-κ curve for associated pipe sections. This value should be representative of the tension a pipe section is expected to encounter during subsequent analyses. As an alternative to specifying an Expected Tension value, PipeLay can be instructed to use the maximum value for a tension criterion, as defined on the Analysis component, to reduce the capacity of the M-κ curve for associated pipe sections; see the Use Criteria Tension option under Material Data Inputs. For a full description of the reduction in M-κ curve capacity due to tension being applied please refer to Technical Note 7. Direct stress/strain curves can also be used to define pipe coating mechanical properties that in turn augment the stiffness of the coated pipe section. More details on this are provided in the coatings discussion later and also in Technical Note 7.
•M-κ and Ramberg-Osgood curves define only bending response. Axial response is assumed to be linear; E is used to compute EA for each pipe section for which the material is used. E is also used for Ramberg-Osgood curve as described below. If a user moment of inertia is defined on the pipe section component the moment of the M-κ curve is scaled by the ratio between the user-input moment of inertia and the calculated moment of inertia, while for the Ramberg-Osgood curve the moment value for My is calculated using this user specified I value as described below.
•The Ramberg-Osgood curve is defined by the equation:
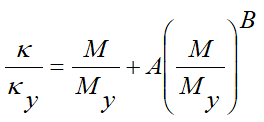
Where ![]() = curvature,
= curvature,
|
= curvature at yield, |
|
= yield stress, |
|
= Young's modulus, |
|
= external diameter, |
|
= bending moment, |
|
= bending moment at yield, |
|
= second moment of area(moment of inertia), can be user specified. |
|
= user inputs defining the Ramberg-Osgood curve. |
|
is a required input when specifying a Ramberg-Osgood curve. |
•The Ramberg-Osgood relationship defines an M-κ curve for each pipe section for which this material is used, since D and I vary from pipe section to pipe section.
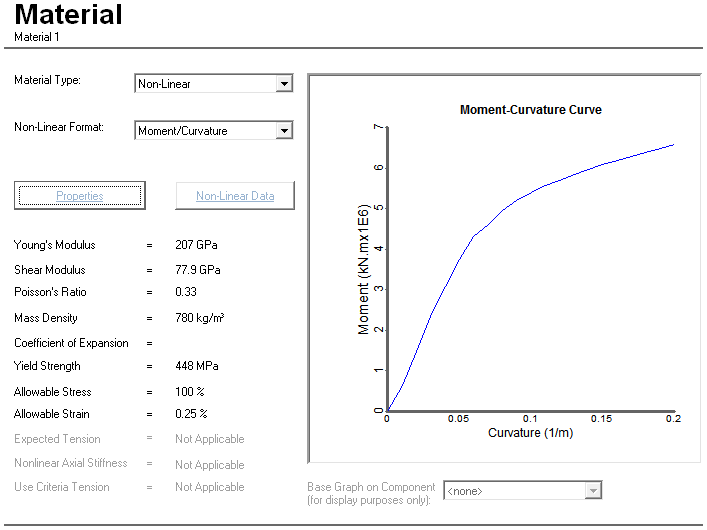
When any non-linear relationship is defined, it can be shown graphically on the right-hand side of the component view, as in the example specification of the figure below. This happens automatically except in the case of a Ramberg-Osgood relationship. Because this relationship can only be graphed for particular D and I values, if you want to plot a Ramberg-Osgood curve you must first select a pipe section on which to base the graph. You do this using the Base Graph on Component drop-down list at the bottom right of the component view. The drop-down list is only available when you select a Ramberg–Osgood specification. The drop-down list displays a list of all of the Pipe Section components in your project, from which you choose one. It is important to stress that choosing this pipe section is only for the purposes of drawing the Ramberg–Osgood graph, and does not tie this non-linear material definition to any particular component.
The dialog for defining non-linear materials also contains input fields similar to the input fields for linear materials such as Mass Density, Poisson’s Ratio, Thermal Expansion Coefficient, Yield Strength, Allowable Stress and Allowable Strain. You input data for these fields in exactly the same way as for linear materials.
A point of note for non-linear M-κ and Ramberg-Osgood material formats is that, as it is not possible to convert moment-curvatures to stresses, the predicted stresses for postprocessing output are computed in the following way:
•The stresses are a product of the estimated bending or von Mises strains and the user specified Young's modulus. This can lead to an over estimation of stresses above the linear limit.