There are four Wave Type options for including a Pierson-Moskowitz spectrum in your dynamic analysis:
▪Pierson-Moskowitz - Equal Area Discretisation
▪Pierson-Moskowitz - Geometric Progression Discretisation
▪Pierson-Moskowitz - Hs/Tp Equal Area Discretisation
▪Pierson-Moskowitz - Hs/Tp Geometric Progression Discretisation
Two of these options nominate the equal area discretisation, while the other two invoke the geometric progression algorithm. For each discretisation option, there are two formats for specifying the spectrum height/period data. For the first format you input the significant wave height Hs and the mean zero up-crossing period Tz; for the second you input Hs and the spectrum peak period Tp. Options 1 and 2 above use the Hs/Tz format, while Options 3 and 4 use Hs/Tp.
The combination of discretisation algorithm and input format you choose determines the dialog you get when you click on the Wave Data button. For example, the first figure below shows the dialog for the Hs/Tz format and the equal area discretisation, while the second figure below shows the Hs/Tp format and the geometric progression discretisation.
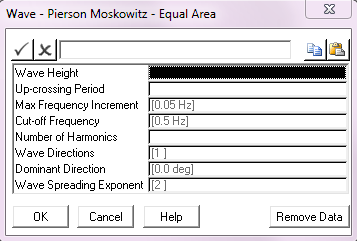 Pierson-Moskowitz Wave Data; Hs/Tz Format, Equal Area Discretisation |
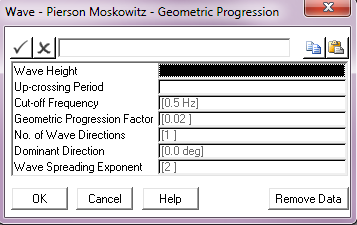 Pierson-Moskowitz Wave Data; Hs/Tp Format, Geometric Progression Discretisation |
All of the entries in these dialogs are described in detail in the Wave Data Inputs article, however some general comments are appropriate here. The wave height and period inputs are self-explanatory. In both dialogs you can optionally specify a Cut-off Frequency; PipeLay does not include any harmonics with frequencies greater than the value here, user-specified or default. In the Equal Area dialog you can specify a Max Frequency Increment, the function of which as previously described is to ensure a sufficient distribution of higher harmonics in the wave elevation time series. The Equal Area dialog also has a Number of Harmonics input which is again self-explanatory, whereas the corresponding entry for the Geometric Progression dialog is Geometric Progression Factor, denoted as r in the previous section.
The final three entries in both dialogs offer the choice between a uni-directional or multi-directional sea. Obviously the default No. of Wave Directions value of 1 gives a uni-directional sea. A multi-directional random sea is defined in terms of a dominant wave direction and the number of wave directions. The dominant wave direction is the direction at which most of the wave energy is concentrated. Its defined in degrees anti-clockwise from the positive sense of the global-Y axis and is denoted θdom. If the number of directions you specify is denoted n, then PipeLay divides a semi-circular arc between (θdom – 90º) and (θdom + 90º) into n equal segments, as shown for example in the figure below, where 3 wave directions are specified. The vector centred on the origin and bisecting the segment defines a wave direction corresponding to each segment. Note that if No. of Wave Directions is even, this process will not result in a wave direction coincident with the dominant, so an odd value is recommended.
PipeLay uses a cosinen spreading function in distributing wave energy between directions in a multi-directional random sea, where n is the Wave Spreading Exponent you define here. The spreading exponent must be an even integer and defaults to 2, giving a cosine2 spreading function.
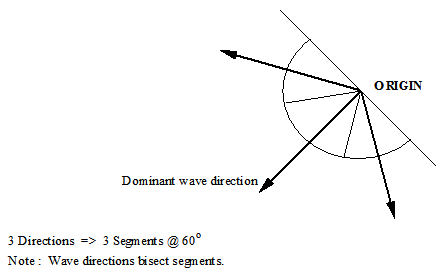
Wave Spreading - Calculating Directions
There are eight Wave Type options for including a JONSWAP spectrum in your dynamic analysis:
▪JONSWAP - Equal Area Discretisation
▪JONSWAP - Geometric Progression Discretisation
▪JONSWAP - Hs/Tz Equal Area Discretisation
▪JONSWAP - Hs/Tz Geometric Progression Discretisation
▪JONSWAP - Hs/Tp Equal Area Discretisation
▪JONSWAP - Hs/Tp Geometric Progression Discretisation
▪JONSWAP - Hs/Tp/Gamma Equal Area Discretisation
▪JONSWAP - Hs/Tp/Gamma Geometric Progression Discretisation
Four of these options nominate the equal area discretisation, while the other four invoke the geometric progression algorithm. For each discretisation option, there are in this case four formats for specifying the wave spectrum data. For the first format you input the spectrum peak frequency fp, the peakedness parameter γ, and Phillips’ Constant α; this might be considered the ‘normal’ JONSWAP format. The second option allows you direct input of significant wave height Hs and mean zero up-crossing period Tz; while for the third format you input Hs and spectrum peak period Tp. The final option is to define a JONSWAP random sea wave spectrum in terms of Hs, Tp and γ. When this format is invoked, the peakedness parameter (gamma or γ) is used in conjunction with a dedicated equation to calculate a suitable value for Phillips’ Constant (α), which in turn is combined with Hs and Tp in a separate equation (derived by ‘Goda’) to determine the wave spectrum.
The Wave Data dialog presented for the various JONSWAP options is similar in many inputs to those for the Pierson-Moskowitz options. For example, the figure below shows the dialog for the case of the ‘normal’ format and the geometric progression discretisation. Other than the first three entries, which are used to define the JONSWAP-specific inputs and are self-explanatory, the remainder of the inputs are the same as explained previously.
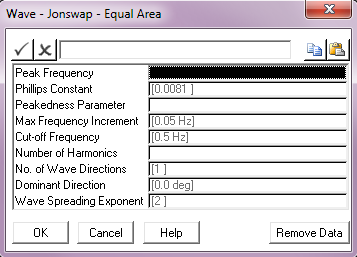
Jonswap Wave Data; Normal Format, Geometric Progression Discretisation
There are two Wave Type options for including an Ochi-Hubble spectrum in your dynamic analysis, corresponding to the two discretisation algorithms:
▪Ochi-Hubble - Equal Area Discretisation
▪Ochi-Hubble - Geometric Progression Discretisation
The Ochi-Hubble wave spectrum model consists of two parts, one for the lower frequency components of the wave energy and the other covering the higher frequency components. Each component is expressed in terms of three parameters; the significant wave height, the peak period and the shape factor. The total spectrum is written as a linear combination of the two. This means that double peaks present in a wave energy density can be modelled, representing for example a (low frequency) swell along with (high frequency) wind-generated waves.
The above is reflected in the format of the Wave Data dialog for either of the Ochi-Hubble options. The figure below shows the equal area discretisation case. The first six entries are the Ochi-Hubble-specific inputs mentioned above (for example, Hs1 is the significant wave height for the lower frequency components). The remaining six entries are as before.
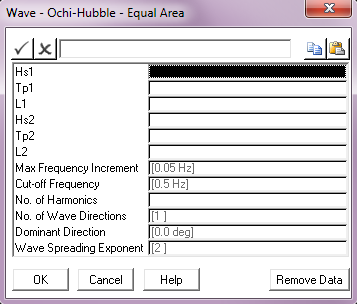
Ochi-Hubble Wave Data; Equal Area Discretisation
There are two Wave Type options for including a Torsethaugen spectrum in your dynamic analysis, corresponding to the two discretisation algorithms:
▪Torsethaugen - Equal Area Discretisation
▪Torsethaugen- Geometric Progression Discretisation
The Torsethaugen spectrum was developed as a double peak spectral model which represents wave conditions in open ocean areas where the waves are dominated by local wind sea, but also exposed to swell.
For both discretisation algorithms the spectrum is specified in terms of significant wave height, peak period and a fetch factor as shown in the dialogs in the two figures below.
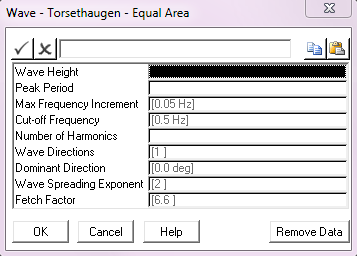 Torsethaugen Wave - Equal Area Specification |
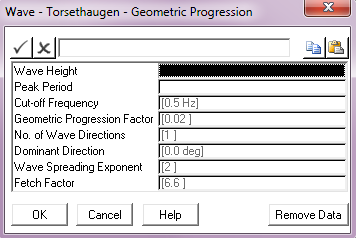 Torsethaugen Wave - Geometric Progression Specification |