
Input |
Description |
Type: |
A drop-down list that allows you to specify the wave type. |
Wave Data |
Click on this button to open a dialog that allows you to enter the wave data. This dialog varies depending on the option you select from the Type drop-down list. The dialogs that are displayed are described in the remainder of this article. |
User Spectrum |
Click on this button to display the Wave – User Spectrum dialog. See the ‘Wave – User Spectrum Dialog’ section in this article for more information. |
Random Seed |
Click on this button to display the Wave – Random Number Seed dialog. See the ‘Wave – Random Number Seed Dialog’ section in this article for more information. |
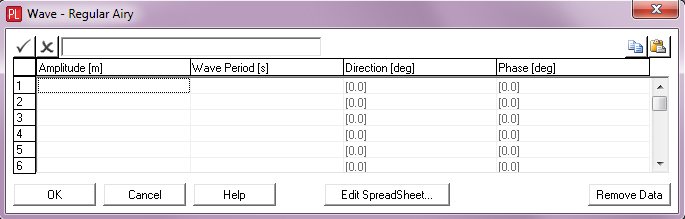
Input |
Description |
Amplitude: |
The regular Airy wave amplitude (MWL to crest or trough). Units: [m] or [ft] |
Wave Period: |
The regular Airy wave period. Units: [seconds] |
Direction: |
The wave direction, measured anti-clockwise from the global Y-axis. All waves in PipeLay emanate from the origin. The default direction is 0°. Units: [degrees] |
Phase: |
The wave phase angle. This input is only appropriate if more than one regular wave is specified. The default phase value is 0°. Units: [degrees] |

Input |
Description |
Height: |
The Stokes V wave height (crest to trough). Units: [m] or [ft] |
Wave Period: |
The Stokes V wave period. Units: [seconds] |
Direction: |
The wave direction, measured anti-clockwise from the global Y-axis. All waves in PipeLay emanate from the origin. The default direction is 0°. Units: [degrees] |
Notes:
(a)If your analysis included vessel response to your Stokes V wave, then using this option means that the response will be fifth order.
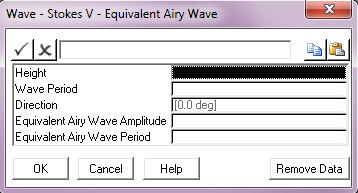
Input |
Description |
Height: |
The Stokes V wave height (crest to trough). Units: [m] or [ft] |
Wave Period: |
The Stokes V wave period. Units: [seconds] |
Direction: |
The wave direction, measured anti-clockwise from the global Y-axis. All waves in PipeLay emanate from the origin. The default direction is 0°. Units: [degrees] |
Equivalent Airy Wave Amplitude: |
The amplitude of an Airy wave used to determine vessel response to the Stokes V wave. The default value is 0. See Note (b) below. Units: [m] or [ft] |
Equivalent Airy Wave Period: |
The period of the Airy wave used to determine vessel response to the Stokes V wave, if this feature is used. The default is the Stokes V wave period. See Note (b) below. Units: [seconds] |
Notes:
(a)If your analysis includes vessel response to your Stokes V wave, then using this option means that the response will be first order (sinusoidal).
(b)You can specify an equivalent Airy wave amplitude without inputting a corresponding period, in which case the Stokes V wave period is used by default. Specification of an Airy wave period without a corresponding wave amplitude is invalid. Of course if an analysis does not include vessel response to waves, equivalent Airy wave parameters are immaterial and unused.
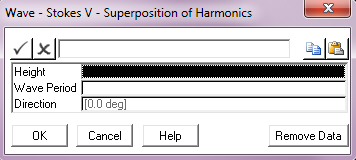
Input |
Description |
Height: |
The Stokes V wave height (crest to trough). Units: [m] or [ft] |
Wave Period: |
The Stokes V wave period. Units: [seconds] |
Direction: |
The wave direction, measured anti-clockwise from the global Y-axis. All waves in PipeLay emanate from the origin. The default direction is 0°. Units: [degrees] |
Notes:
(a)If your analysis includes vessel response to your Stokes V wave, then using this option means that that response will be calculated as a superposition of 5 individual components.

Input |
Description |
Wave Height: |
The Dean’s Stream wave height (crest to trough). Units: [m] or [ft] |
Wave Period: |
The Dean’s Stream wave period. Units: [seconds] |
Direction: |
The wave direction, measured anti-clockwise from the global Y-axis. All waves in PipeLay emanate from the origin. The default direction is 0°. Units: [degrees] |
Eulerian Current Velocity: |
The velocity of the underlying current. This value defaults to 0. See Note (b) below. Units: [m/s] or [ft/s] |
Order of Expansion: |
The order of expansion of the Dean’s Stream Function equations which defines the wave. This value defaults to 15. See Note (c) below. |
Max Iterations: |
The maximum number of iterations to be used in solving the Dean’s Stream function equations. This value defaults to 100. |
Number of Ramp Steps: |
The number of ramp steps over which the wave height is applied. This value defaults to 5. See Note (d) below. |
Notes:
(a)If your analysis includes vessel response to a Dean’s Stream wave, then using this option means that the order of the response will be the same as the order of expansion of the Dean’s Stream Function. Further details are provided in Technical Note 6, ‘Dean’s Stream Function’.
(b)The Eulerian current velocity corresponds to the current recorded by a stationary meter. The principal consequence of an underlying current is a Doppler shift of the apparent wave period.
(c)The order of expansion of the Dean’s stream function is essentially a measure of how non-linear a wave is. In deep water the order can be relatively low (between 3 and 5), while in shallow water the order can be as high as 30.
(d)The Fourier theory formulations used by PipeLay to solve the Dean’s Stream function equation can occasionally lead to multicrested solutions, particularly in shallow water. In order to eliminate this the wave height is gradually increased to the required height in the number of ramp steps specified.
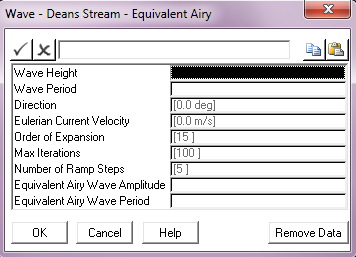
Input |
Description |
Wave Height: |
The Dean’s Stream wave height (crest to trough). Units: [m] or [ft] |
Wave Period: |
The Dean’s Stream wave period. Units: [seconds] |
Direction: |
The wave direction, measured anti-clockwise from the global Y-axis. All waves in PipeLay emanate from the origin. The default direction is 0°. Units: [degrees] |
Eulerian Current Velocity: |
The velocity of the underlying current. This defaults to 0. See Note (b) below. Units: [m/s] or [ft/s] |
Order of Expansion: |
The order of expansion of the Dean’s Stream Function equations which defines the wave. This value defaults to 15. See Note (c) below. |
Max Iterations: |
The maximum number of iterations to be used in solving the Dean’s Stream function equations. This value defaults to 100. |
Number of Ramp Steps: |
The number of ramp steps over which the wave height is applied. This defaults to 5. See Note (d) below. |
Equivalent Airy Wave Amplitude: |
The amplitude of an Airy wave used to determine vessel response to the Dean’s Stream wave. The default value is 0. See Note (e) below. Units: [m] or [ft] |
Equivalent Airy Wave Period: |
The period of the Airy wave used to determine vessel response to the Dean’s Stream wave, if this feature is used. The default is the Stokes V wave period. See Note (e) below. Units: [seconds] |
Notes:
(a)If your analysis includes vessel response to a Dean’s Stream wave, then using this option means that the response will be first order (sinusoidal). Further details are provided in Technical Note 6, ‘Dean’s Stream Function’.
(b)The Eulerian current velocity corresponds to the current recorded by a stationary meter. The principal consequence of an underlying current is a Doppler shift of the apparent wave period.
(c)The order of expansion of the Dean’s stream function is essentially a measure of how non-linear a wave is. In deep water the order can be relatively low (between 3 and 5), while in shallow water the order can be as high as 30.
(d)The Fourier theory formulations used by PipeLay to solve the Dean’s Stream function equation can occasionally lead to multicrested solutions, particularly in shallow water. In order to eliminate this the wave height is gradually increased to the required height in the number of ramp steps specified.
(e)You can specify an equivalent Airy wave amplitude without inputting a corresponding period, in which case the Dean’s Stream wave period is used by default. Specification of an Airy wave period without a corresponding wave amplitude is invalid. Of course if an analysis does not include vessel response to waves, equivalent Airy wave parameters are immaterial and unused.
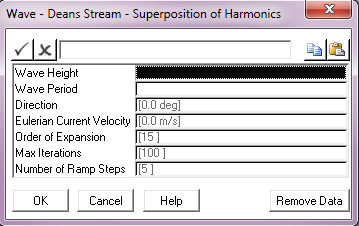
Input |
Description |
Wave Height: |
The Dean’s Stream wave height (crest to trough). Units: [m] or [ft] |
Wave Period: |
The Dean’s Stream wave period. Units: [seconds] |
Direction: |
The wave direction, measured anti-clockwise from the global Y-axis. All waves in PipeLay emanate from the origin. The default direction is 0°. Units: [degrees] |
Eulerian Current Velocity: |
The velocity of the underlying current. This value defaults to 0. See Note (b) below. Units: [m/s] or [ft/s] |
Order of Expansion: |
The order of expansion of the Dean’s Stream Function equations which defines the wave. This value defaults to 15. See Note (c) below. |
Max Iterations: |
The maximum number of iterations to be used in solving the Dean’s Stream function equations. This value defaults to 100. |
Number of ramp steps: |
The number of ramp steps over which the wave height is applied. This defaults to 5. See Note (d) below. |
Notes:
(a)If your analysis includes vessel response to a Dean’s Stream wave, then using this option means that that response will be calculated as a superposition of N individual components, where N is the order of expansion of the Dean’s Stream function. Further details are provided in Technical Note 6, ‘Dean’s Stream Function’.
(b)The Eulerian current velocity corresponds to the current recorded by a stationary meter. The principal consequence of an underlying current is a Doppler shift of the apparent wave period.
(c)The order of expansion of the Dean’s stream function is essentially a measure of how non-linear a wave is. In deep water the order can be relatively low (between 3 and 5), while in shallow water the order can be as high as 30.
(d)The Fourier theory formulations used by PipeLay to solve the Dean’s Stream function equation can occasionally lead to multicrested solutions, particularly in shallow water. In order to eliminate this the wave height is gradually increased to the required height in the number of ramp steps specified.
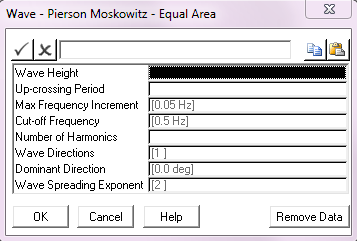
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Up-crossing Period: |
The mean zero up-crossing period Tz. Units: [seconds] |
Max Frequency Increment: |
The maximum frequency increment to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut-off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Number of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. See Notes (b) and (c) below. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0º. |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (c) below. |
Notes:
| (a) | The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area. |
| (b) | A multi-directional random sea is defined in terms of a dominant wave direction and the number of wave directions. The dominant wave direction is the direction at which most of the wave energy is concentrated. A definition of the dominant wave direction, denoted θdom is shown in the 'Dominant Wave Direction' figure below. If the number of directions you specify is denoted n, then PipeLay divides a semi-circular arc between (θdom- 90º) and (θdom+ 90º) into n equal segments, as shown for example in the 'Wave Spreading - Calculating Directions' figure below where 3 wave directions are specified. The vector centred on the origin and bisecting the segment defines a wave direction corresponding to each segment. Note that if Wave Directions is even, this process will not result in a wave direction coincident with the dominant, so an odd value is recommended. |
| (c) | PipeLay uses a cosinen spreading function in distributing wave energy between directions in a multi-directional random sea, where n is the Wave Spreading Exponent you define here. The spreading exponent must be an even integer and defaults to 2, giving a cosine2 spreading function. |
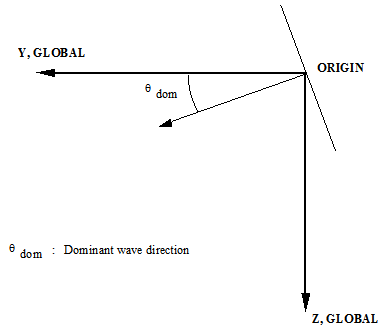
Dominant Wave Direction
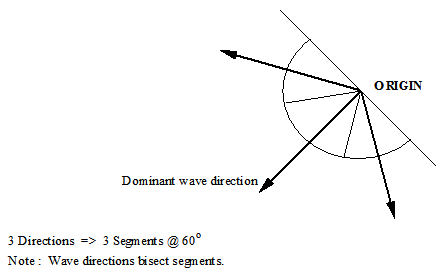
Wave Spreading - Calculating Directions
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Up-crossing Period: |
The mean zero up-crossing period Tz. Units: [seconds] |
Cut-off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No. of Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0º. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
(a)The wave spectrum is discretised into segments based on frequency increments that form a geometric progression.
(b)Refer to the previous menu for a discussion of multi-directional random seas.
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period: |
The spectrum peak period Tp. Units: [seconds] |
Max Frequency Increment: |
The maximum frequency increment to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Number of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0º. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
(a)The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period: |
The spectrum peak period Tp. Units: [seconds] |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No of Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi - directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0º. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
(a)The wave spectrum is discretised into segments based on frequency increments that form a geometric progression.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
Input |
Description |
Peak Frequency: |
The spectrum peak frequency fp. Units: [Hz] |
Phillips Constant: |
Phillips constant α, typically 0.0081 (the default). |
Peakedness Parameter: |
The spectrum peakedness parameter γ. |
Max Frequency Increment: |
The maximum frequency increment. to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut-off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Number of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni directional random sea, greater than 1 gives a multi directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0º. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
| (a) | The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area. |
| (b) | Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas. |
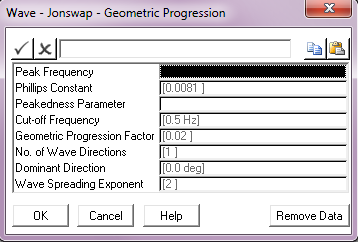
Input |
Description |
Peak Frequency: |
The spectrum peak frequency fp. Units: [Hz] |
Phillips Constant: |
Phillips constant α, typically 0.0081 (the default). |
Peakedness Parameter: |
The spectrum peakedness parameter γ. |
Cut-off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No. of Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0º. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
(a)The wave spectrum is discretised into segments based on frequency increments that form a geometric progression.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
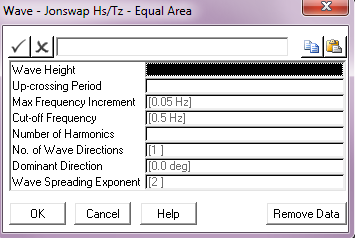
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Up-Crossing Period |
The mean zero up-crossing period Tz. Units: [seconds] |
Max Frequency Increment: |
The maximum frequency increment to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
No. of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0º. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
| (a) | The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area. |
| (b) | Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas. |
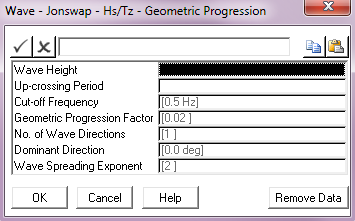
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Up-Crossing Period |
The mean zero up-crossing period Tz. Units: [seconds] |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No. of Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
(a)The wave spectrum is discretised into segments based on frequency increments that form a geometric progression.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
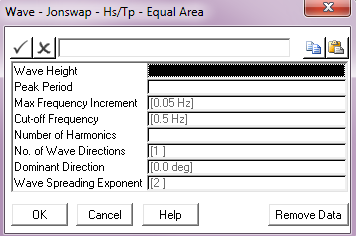
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period |
The spectrum peak period Tp. Units: [seconds] |
Max Frequency Increment: |
The maximum frequency increment in to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
No. of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
| (a) | The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area. |
| (b) | Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas. |
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period: |
The spectrum peak period Tp. Units: [seconds] |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
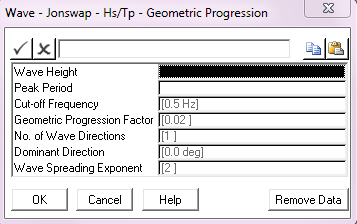
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No. of Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
(a)The wave spectrum is discretised into segments based on frequency increments that form a geometric progression.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period |
The spectrum peak period Tp. Units: [seconds] |
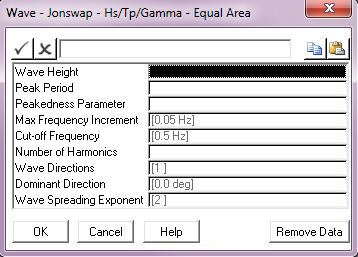
Peakedness Parameter: |
The spectrum peakedness parameter γ (gamma). |
Max Frequency Increment: |
The maximum frequency increment in to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
No. of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
| (a) | The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area. |
| (b) | Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas. |
Input |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period: |
The spectrum peak period Tp. Units: [seconds] |
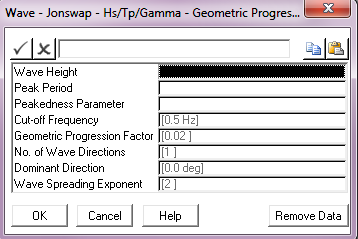
Peakedness Parameter: |
The spectrum peakedness parameter γ (gamma). |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No. of Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. See Note (b) below. |
Notes:
(a)The wave spectrum is discretised into segments based on frequency increments that form a geometric progression.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
Input |
Description |
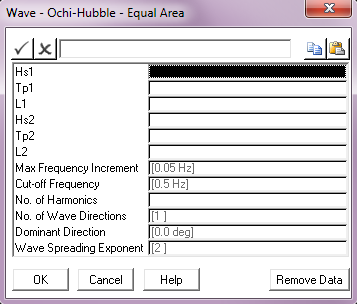
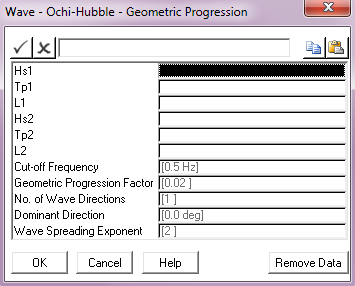
Hs1: |
The significant wave height for the lower frequency components. Units: [m] or [ft] |
Tp1: |
The peak period for the lower frequency components. Units: [seconds] |
L1: |
The shape factor (λ1) for the lower frequency components. |
Hs2: |
The significant wave height for the higher frequency components. Units: [m] or [ft] |
Tp2: |
The peak period for the higher frequency components. Units: [seconds] |
L2: |
The shape factor (λ2) for the higher frequency components. |
Max Frequency Increment: |
The maximum frequency increment in to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
No. of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. |
Notes:
| (a) | The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area. |
| (b) | Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas. |
| (c) | The Ochi-Hubble wave spectrum model consists of two parts, one for the lower frequency components of the wave energy and the other covering the higher frequency components. Each component is expressed in terms of three parameters and the total spectrum is written as a linear combination of the two. This means that double peaks present in a wave energy density can be modelled, representing for example a (low frequency) swell along with (high frequency) wind-generated waves. |
Input |
Description |
Hs1: |
The significant wave height for the lower frequency components. Units: [m] or [ft] |
Tp1: |
The peak period for the lower frequency components. Units: [seconds] |
L1: |
The shape factor (λ1) for the lower frequency components. |
Hs2: |
The significant wave height for the higher frequency components. Units: [m] or [ft] |
Tp2: |
The peak period for the higher frequency components. Units: [seconds] |
L2: |
The shape factor (λ2) for the higher frequency components. |
Cut – off Frequency: |
The cut-off or Nyquist frequency. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No. of Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. |
Notes:
| (a) | The wave spectrum is discretised into segments based on frequency increments that form a geometric progression. |
| (b) | Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas. |
| (c) | The Ochi-Hubble wave spectrum model consists of two parts, one for the lower frequency components of the wave energy and the other covering the higher frequency components. Each component is expressed in terms of three parameters and the total spectrum is written as a linear combination of the two. This means that double peaks present in a wave energy density can be modelled, representing for example a (low frequency) swell along with (high frequency) wind-generated waves. |
Input |
Description |
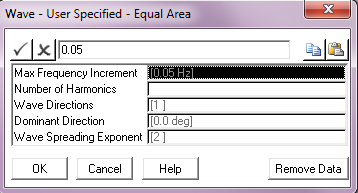
Max Frequency Increment: |
The maximum frequency increment to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Number of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. |
Notes:
(a)The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
Input |
Description |
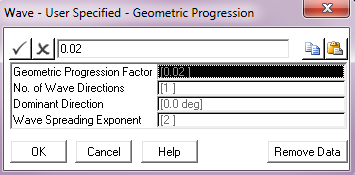
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
No. of Wave Directions: |
The number of wave directions. The default of 1 gives a uni- directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured anticlockwise from the global Y-axis. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This input defaults to 2. |
Notes:
| (a) | The wave spectrum is discretised into segments based on frequency increments that form a geometric progression. |
| (b) | Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas. |
Input |
Description |
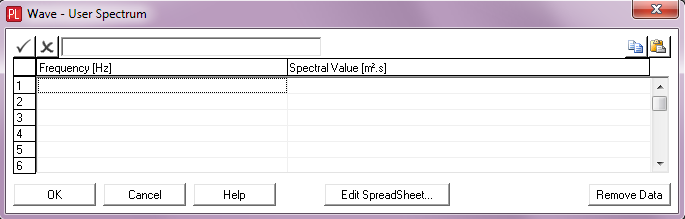
Frequency: |
A frequency value. Units: [Hz] |
Spectral Value: |
The corresponding value of the wave spectrum. |
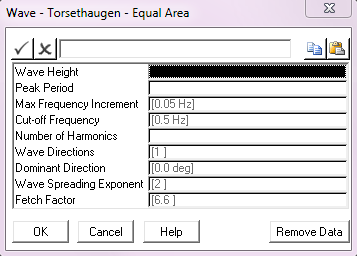
Input: |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period: |
The spectrum peak period Tp. Units: [seconds] |
Max Frequency Increment: |
The maximum frequency increment in Hz. to be used in the spectrum discretisation. This parameter defaults to a value of 0.05 Hz. Units: [Hz] |
Cut – off Frequency: |
The cut-off or Nyquist frequency in Hz. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
No. of Harmonics: |
The number of harmonics to be used in the spectrum discretisation. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured in degrees anticlockwise from the global Y direction. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This entry defaults to 2. |
Fetch Factor |
Factor dependant on fetch. This entry defaults to 6.6. See Note (c). |
Notes:
(a)The wave spectrum is discretised using an approach that divides the area under the spectrum into segments of equal area.
(b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
(c)The suggested value of 6.6 for fetch factor relates to the Metric unit system, in which a factor of 6.6 (m-1/3).s is typically used. If you are using the Imperial unit system, you should adjust the fetch factor accordingly.
(d)The Torsethaugen spectrum was developed as a double peak spectral model which represents wave conditions in open ocean areas where the waves are dominated by local wind sea, but also exposed to swell.
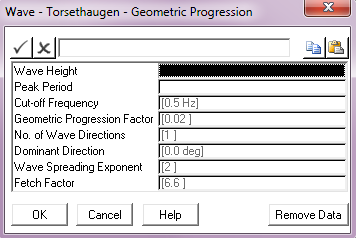
Input: |
Description |
Wave Height: |
The spectrum significant wave height Hs. Units: [m] or [ft] |
Peak Period: |
The spectrum peak period Tp. Units: [seconds] |
Cut – off Frequency: |
The cut-off or Nyquist frequency in Hz. This parameter defaults to a value of 0.5 Hz. Units: [Hz] |
Geometric Progression Factor: |
The geometric progression factor for the spectrum discretisation. This parameter defaults to a value of 0.02. |
Wave Directions: |
The number of wave directions. The default of 1 gives a uni-directional random sea, greater than 1 gives a multi-directional sea. |
Dominant Direction: |
The wave direction in a uni-directional sea, or the dominant wave direction in a multi-directional random sea, measured in degrees anticlockwise from the global Y direction. The default is 0°. Units: [degrees] |
Wave Spreading Exponent: |
The exponent used in distributing wave energy between directions in a multi-directional random sea. This entry defaults to 2. |
Fetch Factor |
Factor dependant on fetch. This entry defaults to 6.6. See Note (c). |
Notes:
a)The wave spectrum is discretised into segments based on frequency increments that form a geometric progression.
b)Refer to the Pierson-Moskowitz – Equal Area Discretisation menu for a discussion of multi-directional random seas.
c)The suggested value of 6.6 for fetch factor relates to the Metric unit system, in which a factor of 6.6 (m-1/3).s is typically used. If you are using the Imperial unit system, you should adjust the fetch factor accordingly.
d)The Torsethaugen spectrum was developed as a double peak spectral model which represents wave conditions in open ocean areas where the waves are dominated by local wind sea, but also exposed to swell.
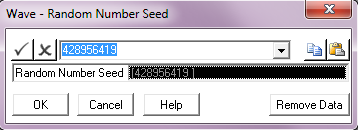
Input |
Description |
Random Number Seed: |
A value to be used as the random number generator seed. |
Notes:
(a)PipeLay uses a random number generator to assign phase values to harmonics in a discretised wave spectrum or spectra. Unless you specify otherwise, PipeLay always uses the same seed value, so that every time you discretise the same spectrum with the same discretisation parameters, you get the same sequence of random phases and consequently the same time history of water surface elevation. You may want to change this, so that you get a different set of phases and so a different wave elevation time history from the same spectrum and discretisation parameters (other than the seed). This can be done by specifying a different seed value here.
| (b) | PipeLay uses a Multiplicative Congruential Generator to generate a sequence of random phases. For best results, the random number seed for this should be a large (and preferably prime) number. You may enter your own value for the random number seed in the dialog box shown above. Alternatively, you can select a seed value from the drop-down list, which you bring up by clicking on the arrow at the side of the dialog box. |
| (c) | Specifying a random number seed is optional. If you do not specify a value, PipeLay uses the first value shown in the list box above by default. |
| (d) | Naturally, invoking this option is meaningful only in the case of a dynamic analysis with a random wave spectrum or spectra. |