This technical note describes the calculation of the various stress outputs provided by PipeLay. These comprise bending, hoop, axial and Von Mises stresses. The calculation of each of these, along with effective tension, is now described in turn.
PipeLay calculates and outputs bending stress at the outer surface of the cross section. The bending stress at a point on the outer surface is defined with reference to Fig. TN.1.1 below as follows:
![]() (TN.1.1)
(TN.1.1)
This relationship is only valid for linear materials. Stress computation for non-linear materials is described below. Bending strains may be computed for non-linear materials as described in Technical Note 2.
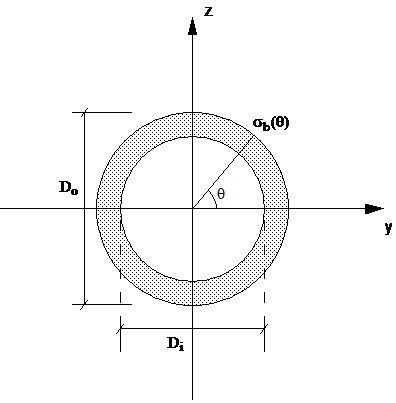
Figure TN.1.1: Calculation of Bending Stress
Here σb(θ) is the bending stress for an angle θ as defined in Fig. TN 1.1; My and Mz are the bending moments about the local y- and z-axes respectively; Iyy and Izz are respectively the second moments of area about the local y- and z-axes; and Do is the effective external diameter.
The maximum value of σb can be found from Eqn. (TN.1.1) by setting ![]() . The value of θ corresponding to the maximum bending stress is given by:
. The value of θ corresponding to the maximum bending stress is given by:
![]() (TN.1.2)
(TN.1.2)
When as is normally the case Iyy = Izz, Eqn. (TN.1.2) reduces to:
![]() (TN.1.3)
(TN.1.3)
PipeLay calculates maximum bending stress using Eqns. (TN.1.2) and (TN.1.1).
PipeLay calculates and outputs hoop stress on the inside surface of the cross section using the relation:
![]() (TN.1.4)
(TN.1.4)
Here σh is hoop stress; Di and Do are the effective internal and external diameters respectively; and pi and po are respectively the internal and external pressures.
Axial stress, which is constant over the cross section, is calculated from:
![]() (TN.1.5)
(TN.1.5)
where σtw is the axial or 'true wall' stress; N is axial force or 'true wall tension'; and A is effective cross section area.
There are three options available in PipeLay for defining non-linear material properties; direct stress/strain input and moment/curvature or Ramberg-Osgood relationship. Full details of their specification can be found in the Material component.
In the case of direct stress/strain defined materials, bending stresses are estimated by computing the bending strains as per Technical Note 2. The stress is then found by looking up the non-linear stress/strain curve. The von Mises stresses are found in a similar manner using the equivalent von Mises strain as described in Technical Note 2 to look up the non-linear curve.
In the case of Moment-Curvature or Ramberg-Osgood defined materials, as the computation of bending strain is based on curvature, bending stresses are estimated by computing the bending strains as per Technical Note 2 and stresses are calculated as a product of the strain and the user specified Young's modulus. This will lead to an over estimation of the stresses above the linear limit.
The von Mises stresses are computed in a similar manner as a product of the equivalent von Mises strain and user specified Young's modulus, which again can lead to an over estimation of stress above the linear limit.