The formulation used by PipeLay in calculating Von Mises stress is derived with reference to Fig. TN.1.2, which shows two equivalent representatives of the in-wall stresses induced by tension and internal and external pressures in a general thick walled riser section.
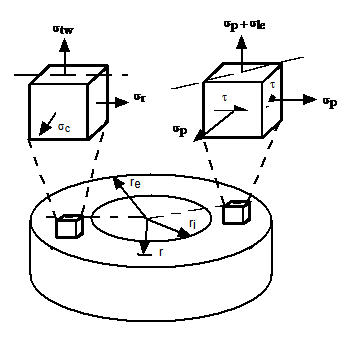
Figure TN.1.2: Riser In-Wall Stress System
In the representation on the left, σtw represents the 'true wall' axial stress as defined in Eqn. (TN.1.5). σc is the circumferential or hoop stress, and σr is the radial stress. σtw is as noted constant over the section, but σc and σr are functions of r, the radius. However, the mean of the two stresses is everywhere constant, and alternative expressions for σc and σr may be written using Lamé's equations as follows:
![]() (TN.1.6)
(TN.1.6)
where
![]() (TN.1.7)
(TN.1.7)
and
![]() (TN.1.8)
(TN.1.8)
Here, pi and po again represent internal and external pressure, and Di and Do are effective internal and external diameters. σp is a constant hydrostatic stress and τ is a distortional shear stress, as shown in the representation on the right in Fig. TN.1.2. The effective stress σle is defined by:
![]() (TN.1.9)
(TN.1.9)
where Teff is the effective tension. Eqn. (TN.1.9) can be rewritten as:
![]() (TN.1.10)
(TN.1.10)
as shown in Fig.TN.1.2. The effective stress is the amount by which the axial wall stress σtw exceeds the in-wall hydrostatic stress σp, and is analogous to the deviatoric term used in solid and soil mechanics.
The Von Mises stress, σvm, for the triaxial system of Fig.TN.1.2 is given by:
![]() (TN.1.11)
(TN.1.11)
Substituting from Eqns. (TN.1.6) and (TN.1.10) gives an equivalent formulation:
![]() (TN.1.12)
(TN.1.12)
The Von Mises stress is therefore closely related to the effective stress, rather than the 'true wall' stress, as would be expected from Eqn. (TN.1.11), since it is obvious that the hydrostatic stress σp can have no effect on the Von Mises stress.
Of course, when the pipe of Fig.TN.1.2 is subjected to bending in addition to tensile and pressure forces, the resultant bending stress (σb say) must be added to σle when calculating σvm. Therefore Eqn. (TN.1.12) becomes
![]() (TN.1.13)
(TN.1.13)
In this case, the Von Mises stress must be checked on the pipe inner surface, where τ is a maximum, and on the outer surface, where σb is a maximum. For this reason PipeLay calculates σvm on both the inside and the outside surface to find the maximum value.
The relationship between axial force N and effective tension Teff is expressed as follows:
![]() (TN.1.14)
(TN.1.14)
Here pi is internal pressure and po is external pressure, and Ai and Ao are correspondingly internal and external areas. In PipeLay, the axial force in an element is a solution variable, and the effective tension Teff is calculated from N using the above relationship. Note that Ao is calculated from the buoyancy diameter Db computed internally by PipeLay, depending on the user specified inputs to the Pipe Section component.
The API-2RD procedure states that for plain round pipe, where transverse shear and torsion are negligible, the three principal stress components are σpr , σpθ and σpz, where r, θ, and z refer to radial, hoop, and axial stress. So σvm is defined as follows:
![]() (TN.1.15)
(TN.1.15)
Moreover, for a thick walled pipe, the radial, hoop, and axial stress may be defined as follows:
![]() (TN.1.16)
(TN.1.16)
![]() (TN.1.17)
(TN.1.17)
![]() (TN.1.18)
(TN.1.18)
Here, t is the wall thickness. t is defined as:
![]() (TN.1.19)
(TN.1.19)
M and I are the resultant bending moments and average second moments of area, respectively. M and I are defined as follows:
![]() (TN.1.20)
(TN.1.20)
and
![]() (TN.1.21)
(TN.1.21)