This approach is an extension of the “single-point moving elastic contact” algorithm described above. The essential difference is the augmentation of bending stiffness of the element(s) in close proximity to the point support. This effectively applies the support over a finite length rather than just at a single point. The direction of support is aligned perpendicular to the pipeline at the support point.
Note that the scale of augmentation referred to above is controlled by the Pivoting Bed Factor specified on the Project component. This factor defaults to 1.2 which effectively means the bending stiffness of elements adjacent to the support point is increased by 20%.
This is the most accurate approach to modelling rollerbox contact, and is essentially a further extension of the “single-point moving contact” algorithm described above. The major extension with this approach is that contact is not restricted to being at a single point on the pipe, but instead is considered to occur over the length of the roller contact surface – in other words, a single rollerbox can contact multiple points on the pipe. This represents the most realistic approach available to modelling pipeline/rollerbox interaction.
With this approach, all nodes in the vicinity of a particular rollerbox are monitored at each iteration for contact with each of the surfaces that make up that rollerbox. For any node that is found to be potentially in contact with the rollerbox, the appropriate stiffness terms (computed from the secant stiffness) corresponding to each of the contact surfaces are incorporated in the global stiffness matrix at the relevant location. The orientation of the stiffness is determined by the instantaneous orientation of the contact surface.
The friction model used with this scheme is essentially the same as that used for the “single-point moving elastic contact” algorithm. The principle difference is that the friction stiffness/load is distributed between all of the nodes on contact with a particular roller contact surface, rather than being applied only at a single contact node.
It should be noted that this elastic contact algorithm differs in a number of crucial respects from that implemented for certain rollerbox types in early versions of the software. Firstly, this algorithm permits contact with any number of arbitrarily orientated contact surfaces simultaneously. Secondly, the contact surface stiffness is incorporated directly in the global stiffness matrix at each node that is in contact with the contact surface. This contrasts with the original approach, where the stiffness is computed by integration along the length of any element in contact with a contact surface. The new approach provides better numerical stability as it is simpler and more appropriate for scenarios that involve only short contact lengths.
This option is very similar to the “single-point elastic contact” approach with the only difference being that the orientations of the individual supports continuously adapt to match the orientation of the pipeline resting on them. This behaviour can be viewed as allowing the support to swivel about its local vertical and horizontal axes, as illustrated in Figure TN.5.4.
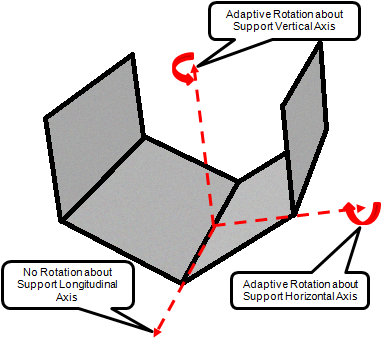
Figure TN.5.4: Roller Contact Model
The benefit of such a model is that the reactions imparted by the support are always in the radial direction of the pipeline, and so do not induce any axial load into the line. Note that such axial loads, if significant, can have a detrimental impact on the effective tension distribution along the pipeline.
The continuous changing of support reaction directions is consistent with what happens in reality when a pipe rests on a single roller, hence the label Roller for the option.
Roller bed supports on lay vessels are often allowed to rotate about a horizontal axis at their centre point and that way the orientation of the beds can conform to that of the pipeline resting on them. If you wish to model such a scenario then the swivel option should be utilised. It allows you to specify which axes you wish the supports to rotate about in order to conform to the orientation of the pipeline resting on them. The local vertical and horizontal axes of a support can be seen in Figure TN.5.4 above. The swivel options available are summarised as follows:
1.No: No swivelling occurs about any axis.
2.About Horizontal Axis: Swivelling occurs about the horizontal axis only.
3.About Vertical Axis: Swivelling occurs about the vertical axis only
4.About Both Axes: Swivelling occurs about both axes.
For the Simple, Standard and Pivoting contact models, where only a single node is in contact with a support at a given time, the orientation of the support depends on the orientation of that contact node. For the Non-Pivoting contact model, where multiple nodes may be in contact with a support, the orientation of the support depends on the average orientation across the nodes in contact with the support. It is worth noting that the Swivel Option need not be used with the Roller contact model as the Roller contact model always swivels about both axes so any Swivel Option selected in conjunction with the Roller contact model is ignored.
Vertical reaction outputs for Support components have a sign convention applied to indicated whether the pipe is pushing down or up into the support surfaces. Positive reactions represent the downward cases whereas negative ones are for upward instances. Such a sign convention can prove useful for Zero-Gap O-Supports and O-Shaped Supports which surround the pipe on all sides, for example at tensioners.
The following points summarise the key aspects of the rollerbox contact model:
•A range of options for modelling rollerbox contact is provided, namely single-point elastic contact, singe-point elastic contact with adaptive support rotations, single-point moving elastic contact, single-point moving distributed elastic contact, and multiple-point moving elastic contact. These provide increasingly more complex (and accurate) contact models.
•The contact algorithm is based on incorporation of contact stiffness terms in the global stiffness matrix, rather than on the application of boundary conditions. This eliminates the energy input phenomenon that is associated with applying boundary conditions, and thus the requirement for very small solution timesteps.
•The incorporation of the stiffness terms is based on the use of a contact ramp, which significantly improves the algorithm robustness and stability.
•The scheme allows the contact stiffness contribution from multiple, arbitrarily-oriented contact surfaces to be incorporated in the global stiffness matrix.